・情報科目をどう勉強すればいいかわからない
・解説を読んでもイマイチわからない。。
この記事では情報科目の試作問題を現役エンジニアが徹底的に解説します。ただ解説をするのではなく、考え方や周辺知識なども伝えていきます。
サンプル問題から最大限に知識を吸収していきましょう!
試作問題はこちらです。
第一問の解説
問1 a b
a問題はSNSやWebサイトの利用に関する問題です。順番に選択肢を見ていきます。
- 0 :
メッセージには早く返信した方がいいかもしれませんが、絶対にすぐに返信しなければいけないわけではないので誤り
- 1 :
正解です。たとえSNSでなどでやり取りしている相手の名前が親友や家族でも、アカウントを乗っ取られていたりなりすましであったりする可能性は0ではありません。
- 2 :
誤りです。匿名で発信した内容でも発信元のIPアドレスなどから情報を特定することができます。当たり前ですが匿名だからといって誹謗中傷などは絶対にしてはいけません。
- 3 :
誤りです。基本的にSNSなどインターネット上に個人情報を書き込むのはやめましょう。非公開グループであっても、そのグループにいる人により情報が流出してしまうことも考えられます。
- 4 :
正解です。これは無意識にやってしまっている人も多いと思いますが、キャラクターの画像を無断でアイコンにすることは著作権の侵害にあたります。
- 5 :
誤りです。芸能人だからと言って肖像権がなくなるわけありません。街で偶然見かけて無断で写真を撮るのは盗撮ですし、ましてやその画像をSNSのあげる行為は肖像権の侵害にあたります。
b問題はインターネット上の情報の信憑性を確かめる方法についての問題です。
- 0 :
誤りです。検索で上位に出てくる記事が正しいとは限りません。お金を払うことで上位に表示させることもできるので内容の信憑性は自分で判断する必要があります。
- 1 :
誤りです。Q&Aサイトは多くの人に支持されている回答が参考になることが多いのは確かです。
しかし自分で大量にアカウントを作って自分の解答を支持することも可能なので、正しい情報と判断する根拠にはなりません。
- 2 :
誤りです。SNSを利用しているといかにも怪しいアカウントの投稿にいいねがたくさんついているのを見かけたことがあると思います。またフォロワーが多いアカウントを買い取ってさぞかし人気のある商品化のように宣伝をするアカウントもあります。
- 3 :
正解です。情報がありふれている中でどの情報を信じるかは自分で決める必要があります。一つだけ参考にしてそれを採用するのではなく複数比較・検討をする必要があります。
問2
問2はパリティビットに関する問題です。またそれに加えて16進数、2進数などの知識も問われています。
まずは空欄エについてです。
- 0 :
誤りです。パリティビットは送信データが奇数が偶数かによって決まるビットです。受信側でパリティビットを再計算することでエラーの検出は可能です。
ただし、そのエラーがパリティビットによるものかデータによるものかの区別はできません。
- 1:
正解です。
01000110は1が奇数なのでパリティビットは1になります。例えば最後の桁が1になると01000111となり、パリティビットは0になります。
最初の桁が1になっても11000110となりパリティビットは0になります。
このようにどのビットが変わっているかをパリティチェックで判別することはできません。
- 2 :
誤りです。選択肢1の解説に書いた通り誤りの位置を検出することはできません。
- 3 :
誤りです。
01000110のパリティビットは1です。このデータの2つのビット(例えば最初と最後)に誤りがあると、
11000111となりますが1の個数は奇数のままなのでパリティビットは変わりません。
このように偶数個の誤りがある場合はエラーを検出することができません。
- 4 :
誤りです。選択肢3で解説したように2つのビットの誤りを検出することはできません。
続いて空欄オについてです。
まずは16進数の7Aを2進数に変換します。手順は以下の画像を参考にしてください。

16進数の7Aは2進数で01111010です。1の個数を数えると5個で奇数なのでパリティビットは1です。
なので011110101となり、選択肢1が正解です。
問3
問3は論理回路に関する問題です。
まず「空欄カ」について見ていきます。(1)の問題文から真理値表を作ってみましょう。
問題文からA,Bの両方が1のときだけ、Xが1になります。真理値表で表すと次のようになります。
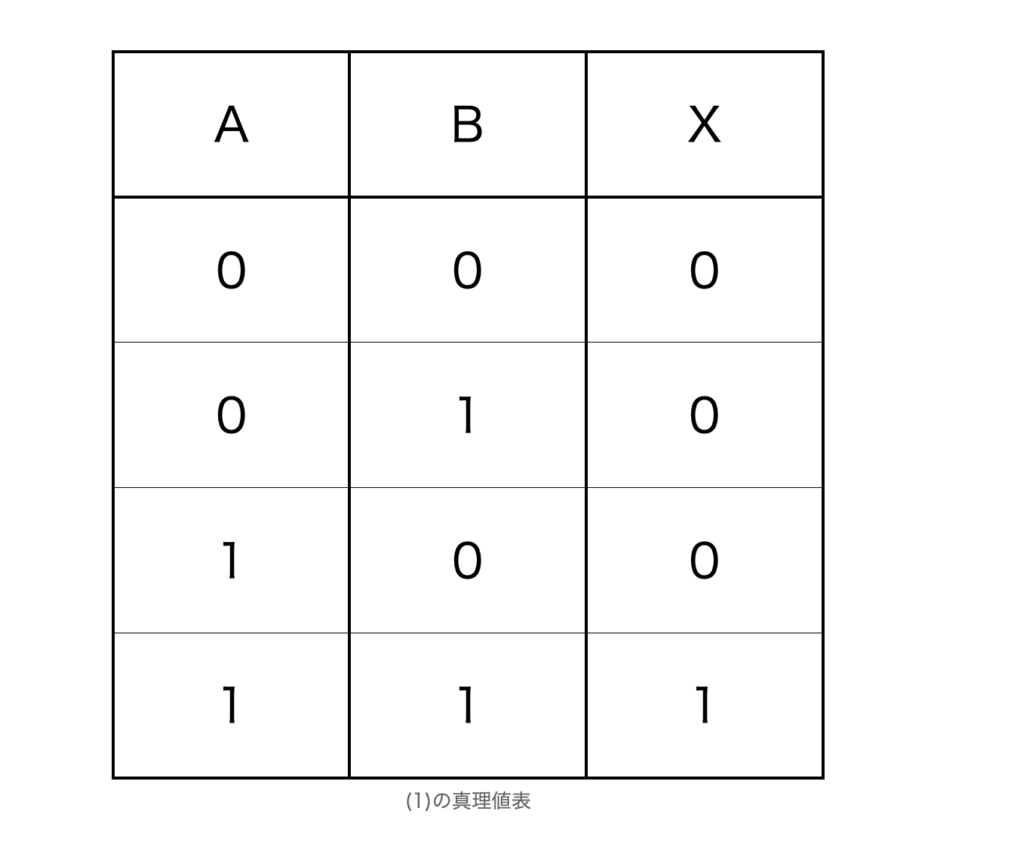
これを問題中の表1 図記号と真理値表と見比べてみると、論理積回路の真理値表と同じであることがわかります。
したがって空欄カには論理積回路を表す回路記号を選択すればいいので、0が正解です。
続いて「空欄キ」について考えます。
(2)の問題文からA,B,Cの内2つ以上1のときにXが1になるとわかります。真理値表を作るときは入力のパターン(今回はA,B,C)を先に書いてからそれぞれの出力を埋めるのが効率的です。
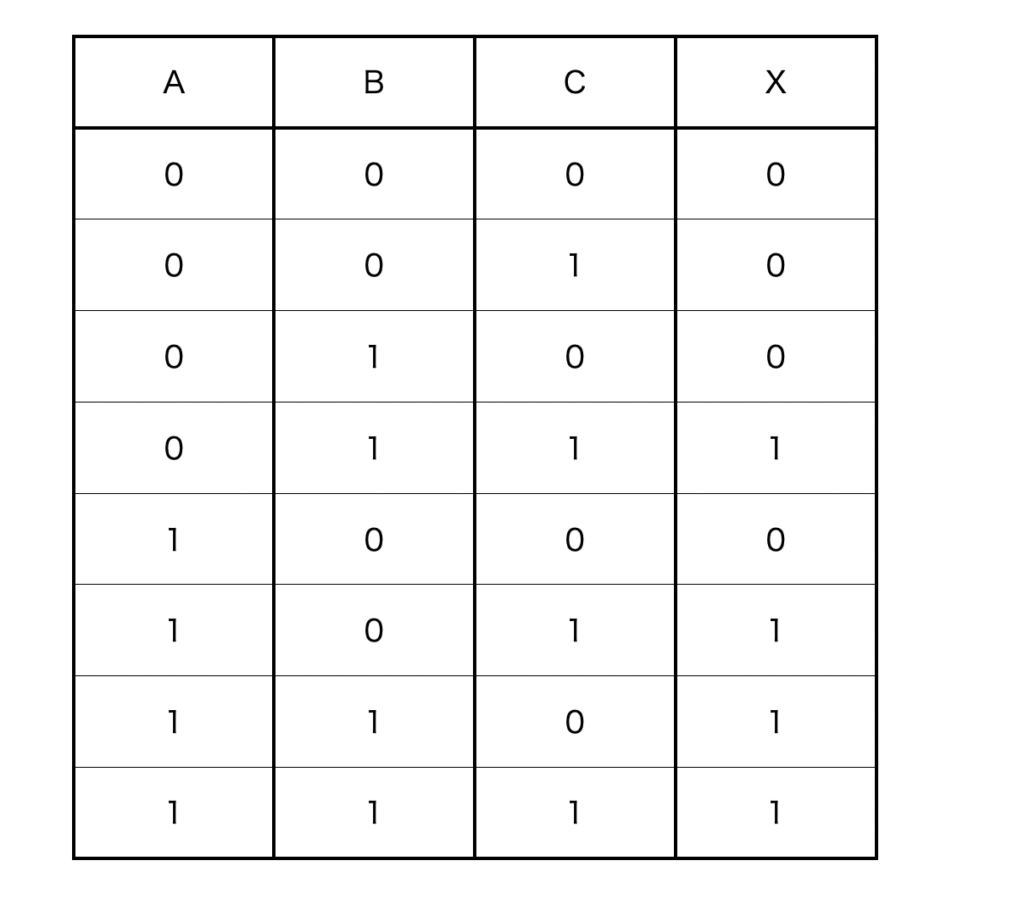
今回は1が二つ以上ある時に出力(X)が1になるように埋めていきます。出来上がった真理値表は以下です。
これを選択肢から選べばいいので正解は2です。
続いて空欄クについてです。
少し複雑ですがまずは空欄クの手前まででみてみます。試しにA,B,Cそれぞれに0,0,1を入れて考えます。この時出力は0になるはずです。
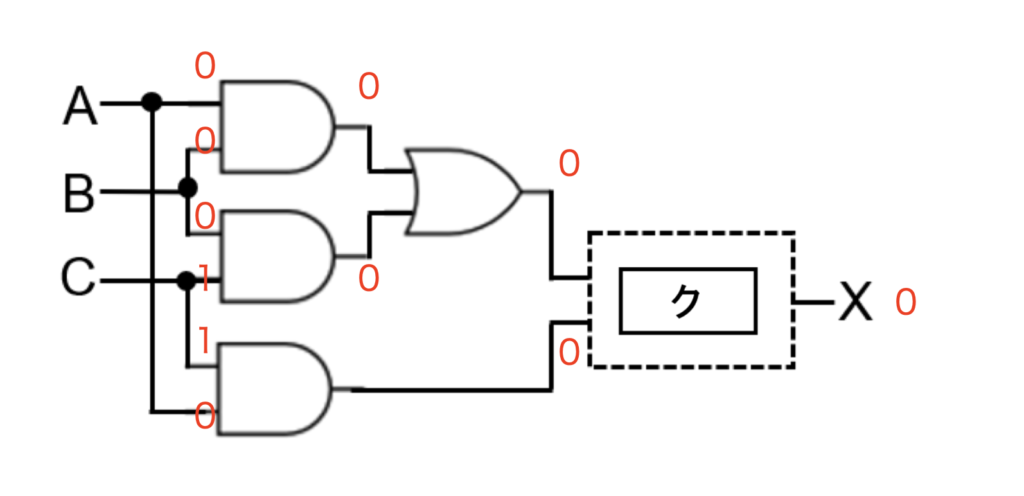
この図からまずクには0,0を入力して0が出力される回路が入ります。選択肢を一つずつ見ていきます。
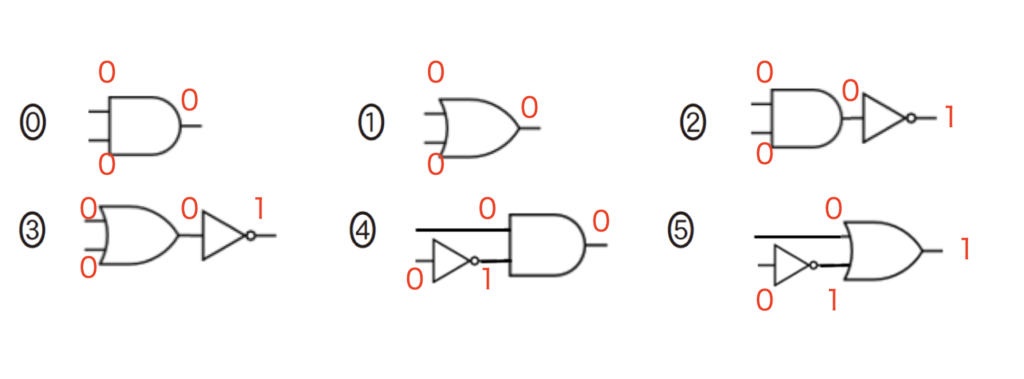
これで1が出力されているものは誤りなので0,1,4のどれかが正解です。
A,B,Cの入力値を他のもので考えてみましょう。次は1,0,1で考えます。
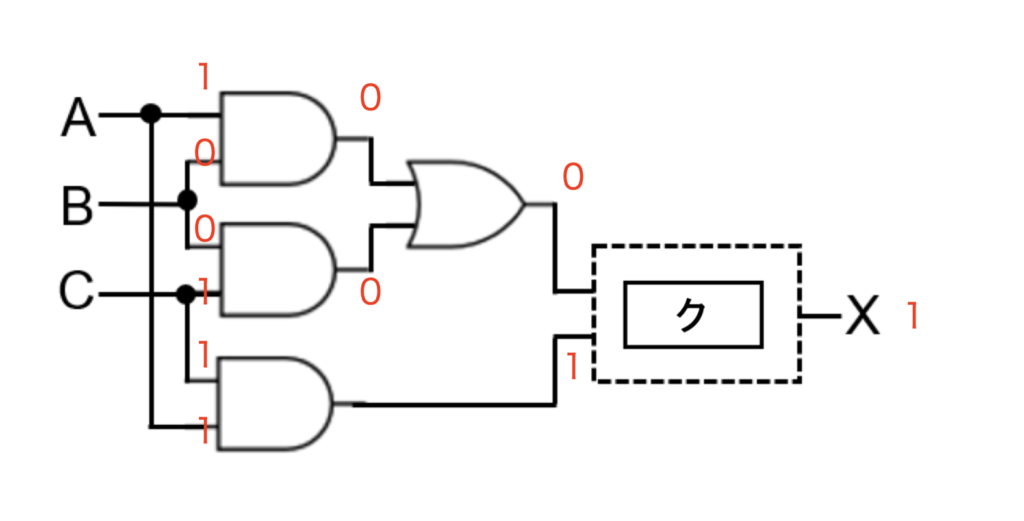
0,1を入力として1を出力するものを探します。
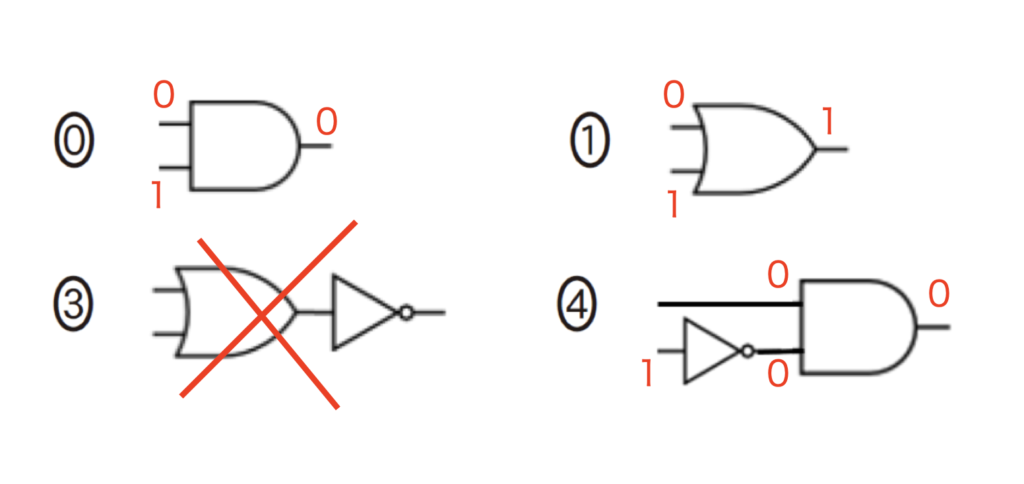
1を出力するのは選択肢1だけなので1が正解です。
問4
問4は情報処理能力の基礎が問われる問題です。
まず空欄ケについてです。
鉄道の路線図に丸で表されているのは駅の場所なので空欄ケは選択肢0が正解です。
次に空欄コとサについてです。
図5は、まずリゾートホテル、シティホテルのようなカテゴリーで整理されています。またそれぞれのカテゴリーを総合評価の高い順に階層で表示しています。
そのため正解の選択肢は3, 4です。
第2問の解説
A-問1
空欄アについてです。この問題は特許権について問われています。
- 0 :
誤りです。使用料が高くなるとQRコードを使う人が減ってしまいます。
- 1:
誤りです。特許権を放棄して誰でも取れるようにすると、次に特許権を取得した人が使用料を引き上げる可能性があります。
- 2 :
誤りです。管理を厳密にするということは、少しでも使う場合はしっかりと申請してお金を払ってから使う必要があることを意味します。よって使う人が増えることにはつながりません。
- 3 :
正解です。特許権は保有していても権利を行使しないので誰でも利用することが可能になります。
A-問2
次に空欄イについてです。
- 0 :
誤りです。円であってもどの角度から見ても比は変わりません。
- 1 :
誤りです。正方形であっても上下左右はありません。
- 2:
正解です。円形にすると解像度によっては線が潰れてしまいうまく読み込むことができなくなってしまうことがあります。
- 3:
誤りです。どの角度からみても黒と白の比が一緒なので目印が斜めに傾いていても関係ありません。
A-問3
続いて空欄ウ、エについてです。
- 0:
誤りです。復元能力7%を見ると、文字数が20から30に増えても2次元コードの大きさは変わっていません。
- 1:
正解です。比例をしているわけではありませんが、文字数が大きくになるにつれて段階的に2次元コードも大きくなっていきます。
- 2:
誤りです。選択肢1のような相関がみられます。
- 3:
誤りです。15文字で考えると7%のセルの数は21× 21 = 441です。30%は29 × 29 = 841です。
4倍もないことがわかります。
- 4:
正解です。同じ文字数の7%と30%を見比べると全てサイズが大きくなっていることがわかります。
必要な情報が増えたぶん、2次元コードの大きさも大きくなっています。
- 5:
誤りです。セルの数は変わっています。
A-問4
空欄オ〜クについてです。
まず空欄オです。同じ文字数では復元能力が大きいほどセルの数が増えます。33 × 33より小さいものは25 × 25しかないので空欄オは2が正解です。
先に空欄クについてです。文字数が最大で復元能力も最大なので一番大きいサイズの1が正解(空欄ク)です。
残りも同様に考えて、カが0、キが3です。
B-問1
B問題はデータの分析です。
空欄ケについてです。生成した乱数と累積相対度数を比較する。例えば乱数が0.31の場合、累積相対度数のどの階級に入るか考えると0.26 < 0.31 <= 0.42なので、階級値が2分の階級に入る。
よって乱数が0.31の時の到着間隔は2分。
同様に乱数が0.95の時を考える。0.94 < 0.95 <= 0.96なので階級値は8分。よって空欄ケには8が入る。
空欄コ〜シは図1(シミュレーション結果)を完成させて考える。
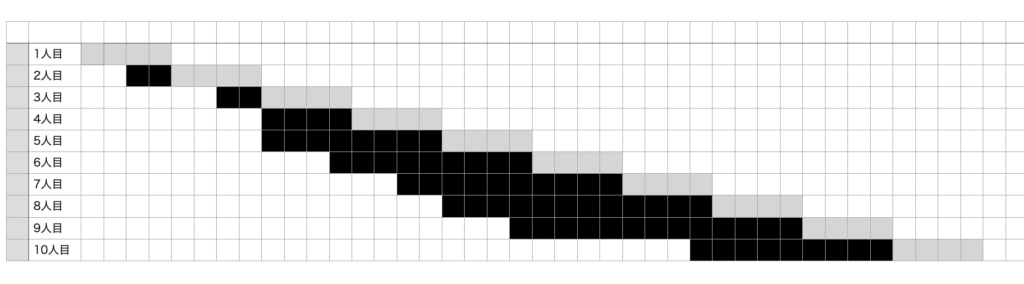
この図の黒い部分が待ち時間なので、最も待ち人数が多いときは4人(6,7,8,9人目が同時に待っている)。したがって空欄コは4が入る。
また待ち時間が一番長かったのは9人目の13分。よって空欄サは1、空欄シは3が入る。
B-問2
これは選択肢を一つずつ検討していきます。読み取れないものを選択することに注意してください。
- 0:
来客人数が10,20,30,40と増えるごとに、最大待ち人数が6,10,13,18と増えています。読み取ることができるので誤りです。
- 1:
来客人数が10人の結果を見ると、最大待ち人数が6人なので来客人数の半分に収まっていません。
読み取ることができないので正解です。
- 2:
来客人数の小さい方から順に、分布のピークは3, 5, 8, 10となっており来客人数の1/4前後になっていることが読み取れるので誤り。
- 3:
散らばりは最大待ち人数から最小待ち人数を引くことで求めることができる。来客人数の小さい方から順に散らばりは6-1=5, 10-2=8, 13-2=11, 23-2=21。
読み取ることができるので誤り。
B-問3
一人当たりの対応時間を減らしたので最大待ち人数、回数ともに小さくなっている結果を選べばいい。
- 0:
正解。
- 1:
変化前とほとんど変わっていないので誤り。
- 2:
最大待ち人数が増えているので誤り。
- 3:
回数が増えているので誤り。
第3問の解説
問1
まずは空欄アについてです。46円の最小の支払い方は問題文中にある通りで、10円4枚、5円1枚、1円1枚、合計6枚です。
なので空欄アは6が入ります。
次に空欄イについてです。
支払う硬貨の枚数とお釣りで受け取る硬貨の枚数の合計が最小になるのは、それぞれの枚数が最小の時です。
なので枚数(51) + 枚数(5)で求めることができます。
したがって、空欄イには0が入ります。
続いて空欄ウ、エについてです。
支払った金額とお釣りをx,yを使って表すと、支払った金額は商品の値段 + お釣りなのでx+yです。
お釣りはyそのものなので、
枚数(x+y) + 枚数(y)を計算すれば良いです。
したがって空欄ウ、エは1と2が入ります。
問2
空欄オとカについてです。
「÷」で整数値の商を求めることができるので、46 ÷ 10を計算すれば46円に10円硬貨を何枚まで使えるか計算することができます。
よって空欄オには2が入ります。
また「%」で割り算のあまりを求めることができるので46 % 10を計算します。
よって空欄カには3が入ります。
次に空欄キ〜コを考えます。
今回はkingakuを46に固定して考えています。iは配列の要素を使う時に使用します。
配列の添字は0から始まるので、配列の中の最大値を使う時にiは4を使います。
今回は配列の中の大きい要素から順に使うので、iの値は4から0まで1ずつ減らします。
したがって、空欄キは1です。
maisuはkingakuを使用する硬貨で割った商を足していくので、maisu = maisu + nokori ÷ kouka[i]で計算できます。
よって空欄クには1、ケには0が入ります。
ここで一つ注意が必要なのが=についてです。数学的に考えるとmaisu = maisu + nokori ÷ kouka[i]は左辺と右辺が等しくないから間違ってると考えてしまいます。
しかしプログラミングにおける=は等しいを表すのではなく代入を表します。ここは大切なので覚えておいてください。
空欄コについてです。
nokoriはnokoriを硬貨で割った余りなので、nokori = nokori % Kouka[I]で計算できます。
したがって、空欄コは1が入ります。
問3
まずは空欄サ、シについてです。
問題文に
「釣り銭無しの場合も含め, 99 円までのすべての釣り銭に対し」
と書かれているので、tsuriを0から99まで1ずつ増やしながら考えます。
したがって空欄サには3、空欄シには0が入ります。
次に空欄ス、セについてです。
これはここまで何回も見てきたように、支払いの枚数とお釣りでもらう枚数それぞれの最小値を足したものを求めればいいので、枚数(shiharai) + 枚数(tsuri)です。
したがって、空欄ス、セは0と2が入ります。
最後に空欄ソとタについてです。
計算した枚数(maisu)とここまでの最小支払い枚数(min_maisu)を比較して、maisuの方が小さければmin_maisuにmaisuを代入します。
したがって空欄ソには0、空欄タには1が入ります。
第4問の解説
問1
一つずつ選択肢を検討します。分析できない仮説を選ぶ問題なので注意してください。
- 0:
1-Aと1-Bがスマートフォンなどの利用時間が短いグループと長いグループで別れているので、二つの表の食事時間を比較することで分析できる。よって誤り。
- 1:
1-Bにスマートフォンなどを使用している時間帯についての情報はないため分析できない。よって正解。
- 2:
学業、趣味・娯楽のデータがあるのでこれらを比較することで分析できる。よって誤り。
- 3:
二つの表の通学時間を比較することで分析することができる。よって誤り。
問2
箱ひげ図から読み取ることができるデータは、最小値、第一四分位数、中央値、第三四分位数、最大値です。
これをもとに選択肢を検討します。
- 0:
睡眠時間が420分以上に、どれくらい分布しているのかを読み取ることはできません。
よって誤り。
- 1:
1-Aでは第三四分位数が550付近にある。したがって学業の時間が550分以上の都道府県は25%程度しかいないため誤り。
- 2:
1-Bにおいて第三四分位数が450より小さいところにあるため、学業時間が450分未満の都道府県は75%以上いることがわかる。
1-Aは中央値がが450より上にあるので学業時間が450分未満の都道府県は50%未満だとわかる。
よって正解。
- 3:
箱ひげ図で中央値は太線で示されている。1-Aと1-Bの中央値がより離れているのは学業時間なので誤り。
問3
AからEを一つずつ検討します。前提として1-Aがスマートフォンなどの使用時間が短いグループです。
- A:
1-Aの値から1-Bの値を引いた数が正ということは、1-Aの値の方が大きいということです。
したがって使用時間が短いグループの方が学業時間が長い傾向にあると言えるので正解。
- B:
Aと同様に考えると、使用時間が短いグループの方が睡眠時間が長い傾向にあるので誤り。
- C:
睡眠時間の図よりも学業時間の図の方が広く分布しているので正解。
- D:
Cと逆のことを言っているので誤り。
- E:
Cと異なる記述なので誤り。
したがって正解はAとCなので空欄ウは0が入ります。
問4
- 0:
散布図を見た時に縦長に分布してれば睡眠の分布のばらつきが多く、横長に分布していれば学業時間の分布のばらつきが大きい。
今回は大体中央に分布しているためどちらともいえない。よって誤り。
- 1:
0と同様に誤り。
- 2:
散布図より学業時間が大きくなる(右に向かう)ほど、睡眠時間は短くなる(下に向かう)ことがわかる。
よって正解。
- 3:
2と逆なので誤り。
問5
まず空欄オについてです。
図6が標準偏差1に変換した図です。標準偏差の2倍は2なので、残差の絶対値が2より大きくなっているデータを数えます。
2つあるので空欄オには2が入ります。
空欄カについてです。
図5を見ると点Pの睡眠時間が大体430くらいだとわかります。このことから図6の1が点Pだとわかります。
よって空欄カは1が入ります。
最後に空欄キについてです。
図6の点1は残差の絶対値が2(標準偏差の2倍)より大きくないことがわかるので外れ値ではないと判断できる。
よって空欄キには1が入る。











コメント